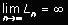Snowflake Curve

In a High School Mathematics class, Vathsala ma’am was telling these words to her students: “If you do not know a particular thing, you should not say that it will not exist or it is impossible.” Suddenly Aparna stood up and asked the ma’am to give her an example. Vathsala ma’am asked Aparna a question: “Can a region of finite area be covered by a curve of infinite length?” Aparna answered as “No ma’am. It’s not possible. How can an infinite length of a line is required to cover say 1 cm2 area? It’s impossible.” Vathsala ma’am replied “This is the example. You do not know that such a thing exists and still you say that it is impossible. It was better if you had said I do not know. In fact there is a curve called Helga von Koch’s snowflake curve. Initially you have an equilateral triangle. The required curve is generated iteratively by adding equilateral triangles to its previous figure’s middle third of each side. It looks like this.”






She continued “This is the curve which is of infinite length but still covers a region of finite area. Students, now you have come to know that such a thing exists, at least try to prove its property. This is your today’s assignment.”

What Vathsala ma’am taught was not only for Aparna or her classmates. It was for all people who would think like Aparna. Try to prove the curve’s property yourself and get to the point which the Great ma’am taught.


Hint 1

If you do not know what to do, try to get the length and area of the final figure as an infinite series. The length should tend to infinity and the area should converge to a finite value.


Hint 2

Use Limits.


Answer

The length of the snowflake curve tends to infinity. If the side length of the initial triangle is a units, then the area of the region covered by the curve is




Solution

Initially assume that the initial triangle is of side 1 unit. In the following discussion we use the term side to mean an edge.

Define some notations. Let,










The problem is simple. It asks us to show that




In Mathematics, the above conditions are written as





Let us find some formulae for S and N








a) Here we shall prove



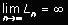
Find this by yourself




On substitution (by top down or bottom up approach), we get




Applying limits, we have











Alternative Method















Continuing from here as above, we get the desired result.


b) Here we shall prove















Applying limits, we have







If the side of the initial triangle was a units, prove that





There are many curves similar to the aforementioned curve. Ex:


















Find out more about these kinds of curves which come under a broad class of curves called fractals and find out their applications.

Though we have mathematically solved the problem of Vathsala ma’am, even now it is very difficult to believe that a finite area can be enclosed by a line of infinite length. So whenever we do not know a particular thing, we should not say that it is impossible or its not there.